Как правило, у большинства учеников самый нелюбимый блок в экзаменах — геометрия, потому что он тяжело даётся. А кто-то и вовсе его не понимает. А в геометрии есть самый нелюбимый тип заданий — это задачи на доказательство. Почему так происходит и как помочь ученику научиться их решать?
 Задачи на доказательство: как научить школьника решать любую
Задачи на доказательство: как научить школьника решать любуюЧто такое задача на доказательство
Задача на доказательство — это утверждение, которое нужно доказать, используя различные теоремы, аксиомы, следствия и признаки геометрии. Другими словами, нам нужно решить задачу и получить то же самое, что написано в условии, тогда задание будет выполнено. Поэтому задачи на доказательство на самом деле несильно отличаются от задач на нахождение чего-либо — просто то, что нужно найти, уже известно заранее. Звучит даже легче, не правда ли? Так почему же многие школьники всё равно намеренно пропускают эти задания и не решают их?
Всё дело в том, что задачи на доказательство очень похожи на то, как доказываются теоремы. А доказательство теорем начинается в 7 классе, когда происходит деление на Алгебру и Геометрию как отдельные предметы в школах. Однако обычно доказательство теорем выглядит следующим образом:
- учитель доказывает теорему у доски,
- ученики переписывают себе всё в тетрадь, иногда даже не понимая, что они пишут,
- дальше звучит знакомая всем фраза «Выучите доказательство, потом ответите его на оценку»,
- а дальше зачастую происходит зубрёжка переписанной теоремы.
Даже человек без педагогического образования догадается, что к пониманию, как осуществляется доказательство, это не приведёт. Да и зачем, если ни на одном экзамене не просят доказывать теоремы? Наоборот, нужно просто использовать уже готовые и доказанные формулировки. Но навык это очень полезный, и вот почему.
Где мы встречаемся с доказательствами
Умение доказывать геометрические задачи проверяют 2 главных школьных экзамена по математике — ОГЭ и ЕГЭ.
- В ОГЭ доказательство находится в № 24 как самостоятельная задача, которая приносит 2 балла максимум,
- в ЕГЭ доказательства встречаются в пунктах а) в № 13 (стереометрическая задача) и № 16 (планиметрическая задача), которые сами по себе приносят по 1 баллу, но без корректных доказательств практически невозможно перейти к пункту б) с решением, что в совокупности приносит по 3 балла за каждую задачу.
Как вы можете заметить, доказательства достаточно важны и приносят неплохие баллы сдающим экзамены. Но это не единственная их польза. Все задания на доказательство помогают ученикам выстраивать логические цепочки и учат рассуждать, а это пригодится не только на экзаменах, но и в жизни.
Так как помочь школьникам научиться их решать?
Как научить школьника решать задачи на доказательство
Доказательство, как я уже говорила, несильно отличается от решения всех геометрических задач. Алгоритм в обоих случаях такой:
- построить чертеж,
- отметить на чертеже, что дано,
- отметить на чертеже, что нужно найти,
- построить логическую цепочку от того, что нужно найти до того, что дано,
- записать шаги доказательства.
Кроме того, в ходе решения или доказательства нужно не забывать выносить всю теорию на чертёж, а также строить чертеж, причем как можно большего размера — так будет лучше видно детали.
Но вернёмся к объяснению задач на доказательство ученикам. Самое главное — объяснить, как должно строиться доказательство, потому что именно здесь у учеников возникают проблемы. Обычно они двух видов:
- слабые ученики просто не берутся за доказательство, потому что не понимают, что делать,
- а сильные в ходе доказательства могут опускать и не расписывать некоторые важные пункты, потому что для них они кажутся очевидными, что приводит к нарушению логики и потере баллов.
Удобная аналогия для решения задач на доказательство
А секрет прост. Доказательство должно быть похоже на заплетание косички:
- три пряди, на которые мы делим все волосы — это то, что нам дано,
- готовая косичка — то, что должно получиться или то, что нужно доказать,
- процесс вплетания прядей — построение логической связи.
Заметили сходство с алгоритмом выше?
Если вы сможете донести это до учеников, то проблема с пропуском важных этапов решится. Ведь мы не можем пропустить прядь, пока плетём косичку? Тогда она у нас просто не получится.
Если пример с косичкой не поможет, то можно провести аналогию с объяснением доказательства очень-очень слабому ученику. Нужно посоветовать ему представить, что, записывая доказательство, он объясняет его другу, который ничего не понимает и всегда задаёт один и тот же вопрос «Почему?». Тогда «отвечая» каждый раз на «Почему?», ученик автоматически будет всё подробно расписывать, а у эксперта при проверке такого вопроса не возникнет.
Давайте объединим все вышеуказанные приёмы и алгоритм и разберём несложную задачу на доказательство. Я буду писать объяснение от первого лица, которое вы можете использовать на уроке, и к нему иногда добавлять поясняющие комментарии.
Разбор задачи на доказательство
Шаг 1. Понять, что нам дано
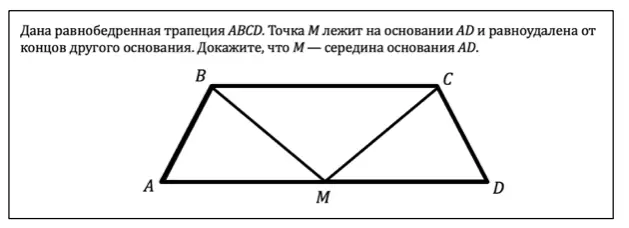 Задача на доказательство, которую мы будем разбирать дальше
Задача на доказательство, которую мы будем разбирать дальшеК счастью, первый пункт алгоритма можно опустить, потому что чертёж нам уже дан. Далее нужно вынести на чертёж всё что дано, а именно:
- АВ = CD, так как по условию трапеция равнобедренная, а значит её боковые стороны равны,
- ВМ = СМ, так как точка М равноудалена концов основания ВС.
Шаг 2. Понять, что нужно доказать
Теперь отмечаем то, что нужно доказать:
- нужно доказать, что М — середина AD, а значит отрезки АМ и MD должны быть равны.
Итак, получается следующая картина:
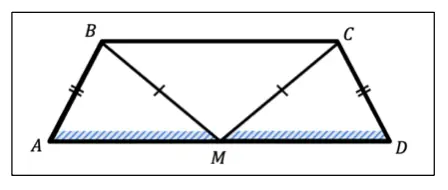 Вот это нужно доказать в задаче
Вот это нужно доказать в задачеА теперь нужно построить логическую цепочку от того, что нужно найти, до того, что дано.
Я не оговорилась, нужно идти от вопроса к тому, что есть. Скажите ученикам, чтобы они представили, будто раскручивают клубок с рассуждениями, а когда дойдут до точки начала, будут закручивать его обратно и записывать всё по порядку. Кстати, вот вам ещё один приём, который поможет научить учеников доказывать задачи.
Шаг 3. Выстроить логическую цепочку
- Итак, как мы можем доказать, что AM = MD? Верно, из треугольников ABM и MCD, ведь если мы докажем, что данные треугольники равны, то и все их элементы тоже будут равны. Сейчас мы раскрутили первый виток нашего клубочка.
- Как нам доказать, что треугольники ABM и MCD равны? Правильно, у нас уже есть две равные стороны, осталось доказать, что углы ABM DCM равны. Ещё виток раскрутили!
- А как доказать, что углы ABM DCM равны? Конечно, можно воспользоваться свойством равнобедренной трапеции, а также получившимся равнобедренным треугольником ВМС. Вот мы и раскрутили клубок! А теперь будем его закручивать, подробно всё расписывая.
Не забывайте про ученика-почемучку, которому вы как будто объясняете доказательство. А также не забудьте в решение выписать всё то, что вы уже вынесли на чертёж, начинать нужно именно с этого.
- ВМ = МС по условию, следовательно треугольник BMC — равнобедренный, значит углы МВС и МСВ равны.
- Углы АВС и BCD равны (почему?), как углы при основании равнобедренной трапеции ABCD.
Из п. 1) следует, что углы МВС и МСВ равны, значит углы АВM и DCM равны (почему?), так как АВM = АВС — МВС, а DCM = BCD — МСВ. - ВМ = МС по условию,
АВ = CD (почему?), как боковые стороны равнобедренной трапеции,
углы АВС и BCD равны по доказанному в п. 2), следовательно треугольники ABM и MCD равны (почему?) по двум сторонам и углу между ними (очень важно указать признак, по которому треугольники равны). - Так как треугольники ABM и MCD равны, то AM = MD.
Что и требовалось доказать.
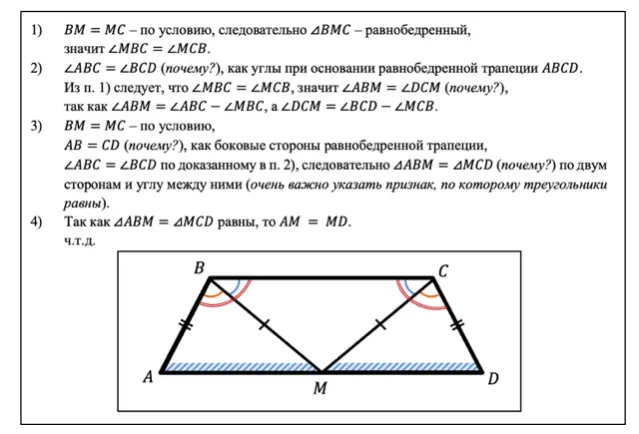 Решение задачи на доказательство вместе с чертежом
Решение задачи на доказательство вместе с чертежомВот так легко мы доказали задачу, используя:
- алгоритм решения геометрической задачи,
- косичку,
- ученика-почемучку
- и клубочек.
Теперь вы знаете, как объяснить доказательство самому слабому ученику, а также как подсказать сильному, чтобы он не упускал важные факты. И пусть мы разобрали задачу уровня ОГЭ, в ЕГЭ на более сложных примерах все эти принципы работают с таким же успехом.