В ЕГЭ по физике примерно 11 задач по механике, включая три сложные задачи из второй части. Так получилось потому, что этот раздел науки в школьной программе изучают дольше всего.
Хорошо разбираясь в механике, можно набрать достаточно большое количество баллов! Мы разберем один из часто встречающихся типов задач.
С чего начать
Все задачи по механике можно условно разделить на четыре раздела (плюс один дополнительный). Это задачи типа 3-8 в бланке ЕГЭ:
- описание движения (кинематика),
- сила и импульс (динамика),
- работа и энергия (механическое действие),
- условия равновесия и рычаги (статика, механизмы),
- дополнительный раздел “Механические колебания” (маятники).
В сложных задачах механика может встретиться в заданиях типа 25, 26: одна из них качественного характера, другая расчётная.
Последняя задача строго механическая и считается самой сложной — за нее дают аж 4 первичных балла. Также механика часто встречается там, где комбинируют два раздела физики, например: механика и термодинамика, или механика и электричество.
Поэтому учителю при подготовке ученика к ЕГЭ стоит много времени уделить именно механике – уж очень много баллов можно собрать именно с этого раздела.
В этой статье мы обратим внимание на те задачи, которые могут попасться в типе задач 3, 5-8 в первой части и 25, 30 во второй части.
Задачи на броски
Часто встречающийся формат задач – это броски. Они делятся на два основных вида:
- броски ровно вертикально,
- броски под углом к горизонту.
При этом сразу отметим, что можно применять в решении два основных подхода: систему уравнений движения и закон сохранения энергии.
Задачи на броски вертикально вверх
Здесь четыре типа движения:
- падение объекта,
- бросок объекта вниз,
- бросок объекта вверх,
- бросок объекта с определенной высоты.
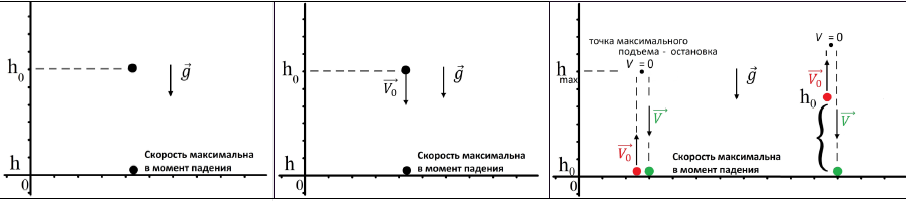Подпись к фото: на схемах изображены все типы движения При любом из типов вертикального движения мы можем использовать систему уравнения движения. Давайте выведем, например, для случая «бросок вверх» максимальную высоту подъема через скорость и ускорение, ведь ускорение нам известно (g примерно 10):
А теперь найдем выражение для той же самой высоты, но уже через закон сохранения энергии, зная, что вся кинетическая энергия перейдет в потенциальную:
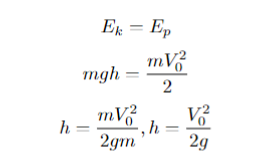
Как мы видим, формулы идентичные. Следовательно, при решении задач можно использовать либо один подход, либо другой.
Но главное, что нужно понимать: скорость будет соответствовать высоте. Необязательно брать начальную скорость и максимальную высоту, можно взять изменение высоты и изменения скорости:
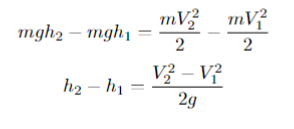
Это вывод нужно обязательно показать ученику, ведь гораздо проще понять смысл и запомнить, как решаются задачи или какие принципы используются, если есть доказательства и пояснения.
Стоит отметить, что применять уравнения движения мы можем абсолютно всегда. Но когда речь идет о законах сохранения, мы можем применять их только тогда, когда система замкнутая, то есть нет воздействия внешних сил.
Лайфхак: можно посоветовать ученику при чтении условия обратить внимание на то, что в задаче дано.
— Если в задаче не дано время, то, скорее всего, данную задачу можно решить двумя способами, и быстрее вывести уравнение через закон сохранения энергии.
— Если же есть время, то лучше воспользоваться уравнением движения, а потом проверить с помощью закона сохранения.
Задачи на броски под углом к горизонту
Броски к горизонту бывают всего двух типов. Либо бросают с какой-то высоты (чаще всего горизонтально), либо бросают с поверхности земли под углом (бывают еще броски из ям, но такие задачи в ЕГЭ крайне редки).
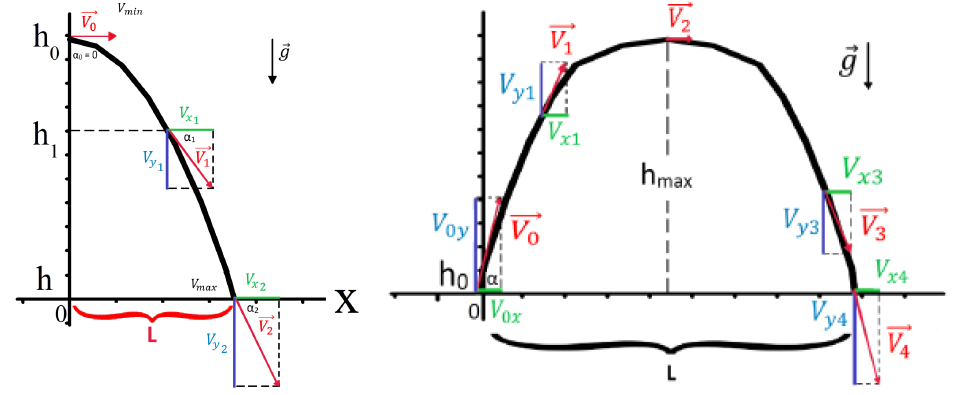
Важно пояснить ученику, что в таких типах задач ничего принципиально другого нет. Единственное — мы должны рассматривать в таких задачах два типа движения.
Стандартное равномерное движение по оси Х и с ускорением вертикальное по оси У. А также скорость, которая была в формулах ранее, изменится на две составляющие — по оси Х и по оси У:
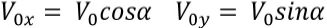
Все остальное останется таким же, и в итоге мы получаем следующую формулу для максимальной высоты:
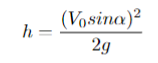
Примеры задачи
Рассмотрим, как применить эти два метода, чтобы решить задачи из ЕГЭ.
Тело брошено вертикально вверх. Через 0,5 с после броска его скорость 20 м/с. На какой высоте окажется тело? Сопротивлением воздуха пренебречь. (Ответ дайте в метрах.)
Сначала решим методом уравнения движения:
А теперь решим с помощь закона сохранения энергии:
Единственное, что нужно учесть — при уменьшении кинетической энергии увеличивается потенциальная, поэтому в конце минус пропадает.
Таким образом, мы получили одинаковые ответы двумя способами.
Краткий вывод
Такого рода задания достаточно часто встречаются в ЕГЭ как в первой, так и во второй части, поэтому важно знать два метода решения, чтобы у ученика были запасные варианты проверки правильного ответа.
И помните: «Fortis fortuna adiuvat» — удача на стороне сильных. Старайтесь, и все будет хорошо!